Map Projection Animations
As per statement in chapter Cartography there are diverse types of systematizations of map projections.
Primarily we mention the differentiation according to the type of the projection surface resp. auxiliary surface (plane, cone, cylinder) (see True Projections), according to the differential-geometrical characteristics (partial length-preserving, equal-area, conformal), according to the position of the projection axis, etc..
Map projection animations present a particular view of specific similarities among map projections or whose differences (see also [13] among Literature). The so called Continuums which are presented here are based primarily upon the variation of single projection parameters (as e.g. continously varied standard parallels)
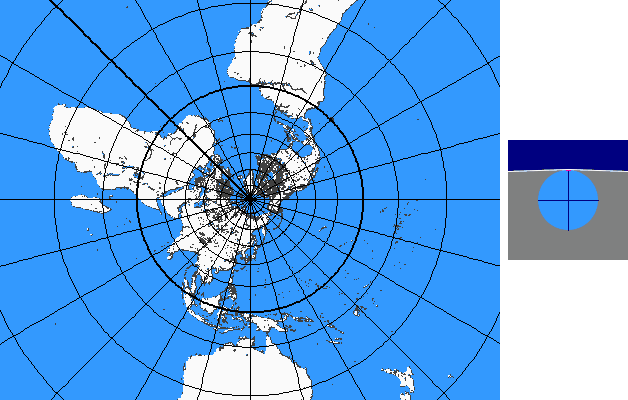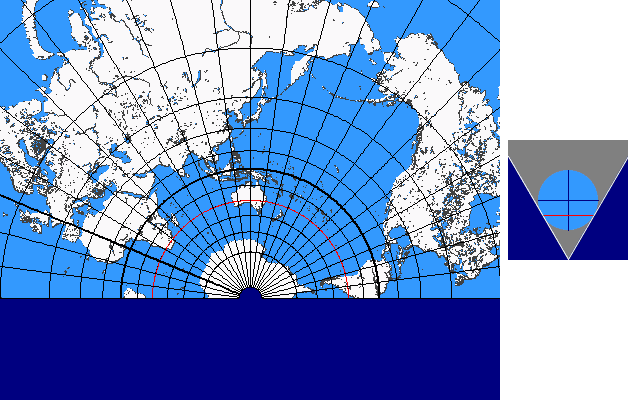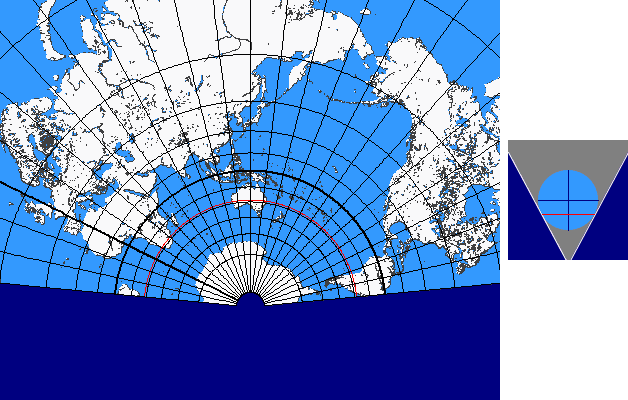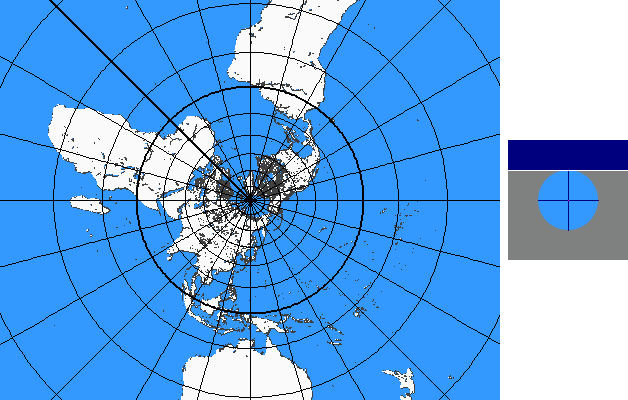
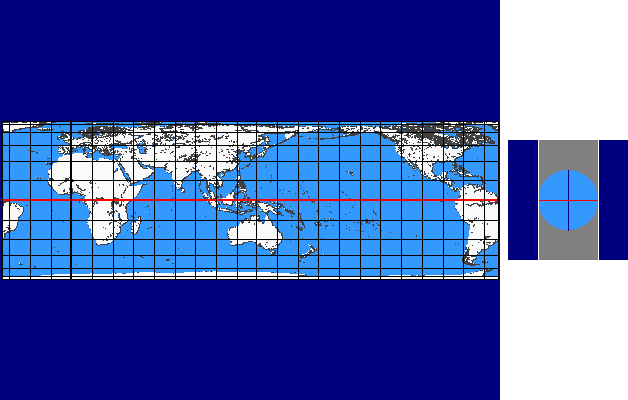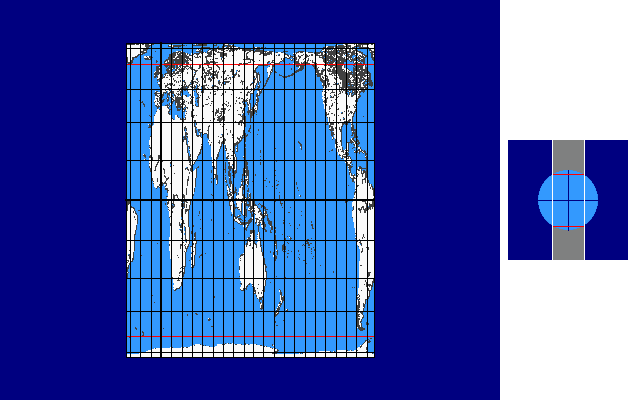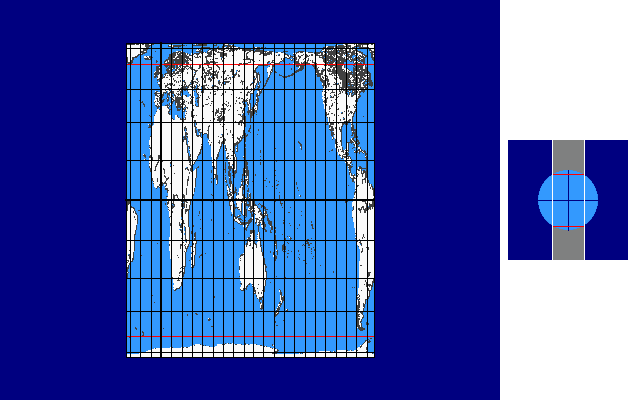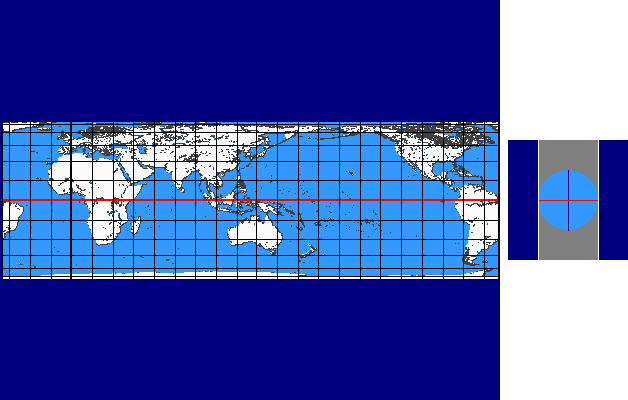
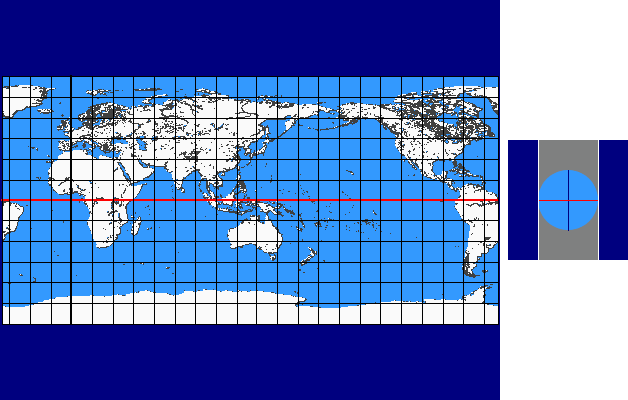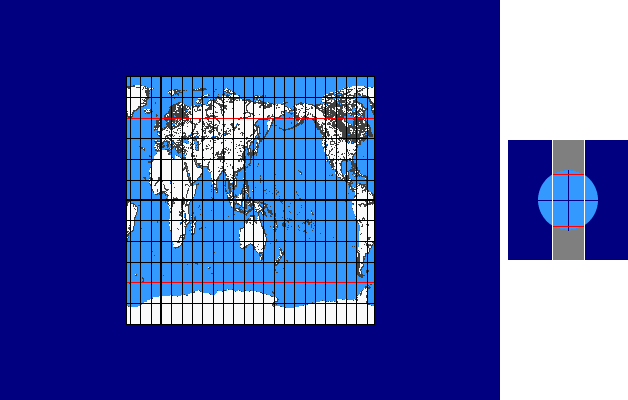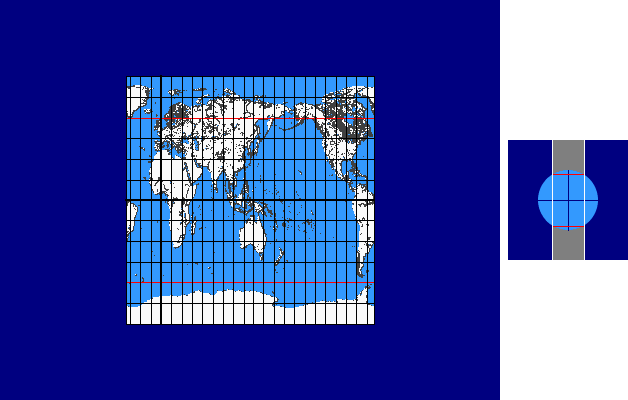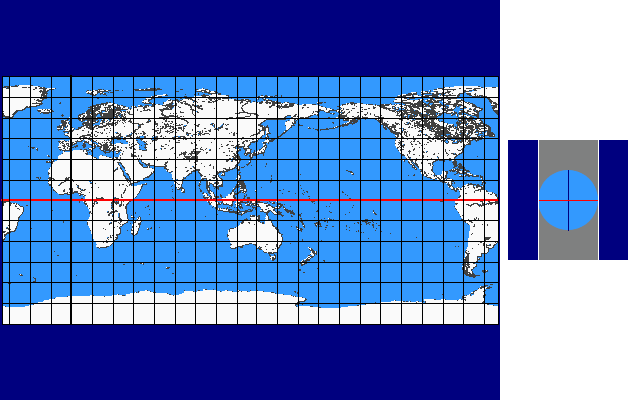
Perspective Continuum
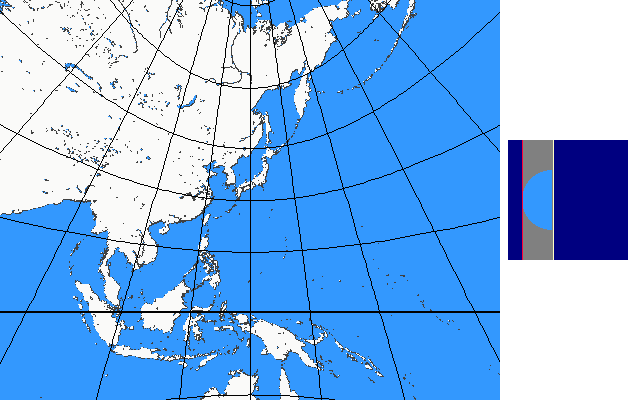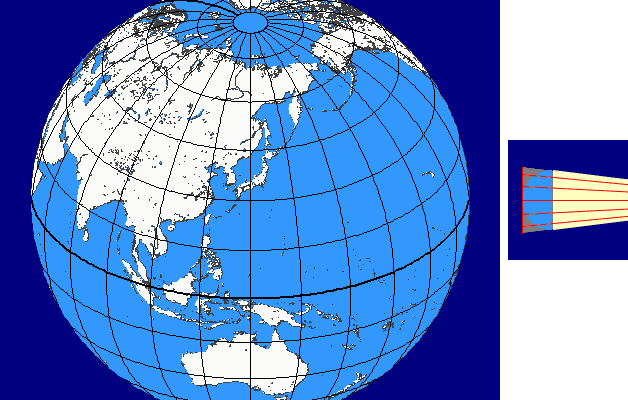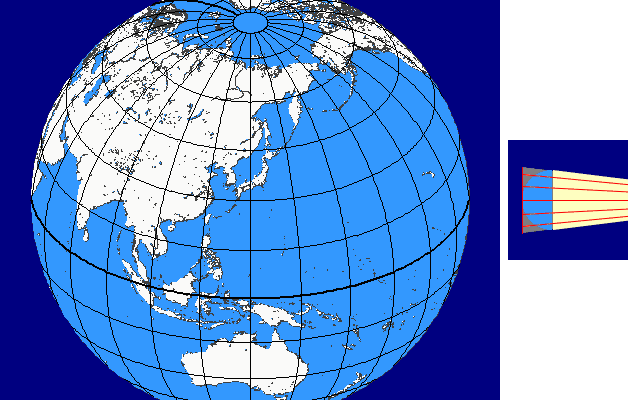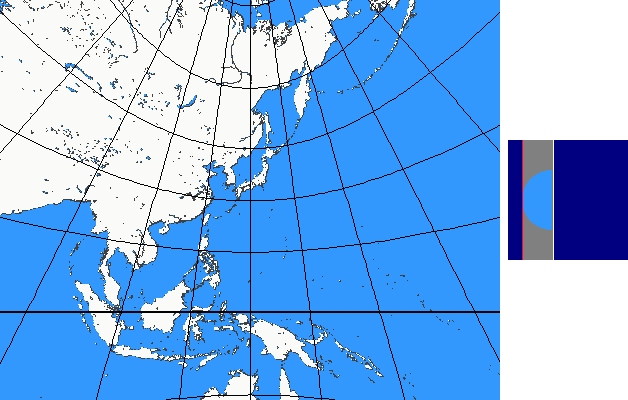
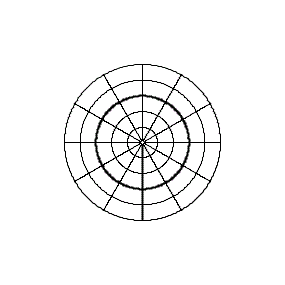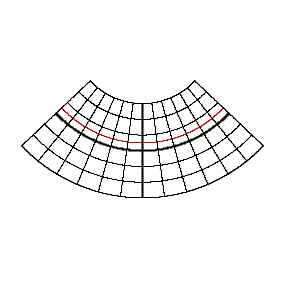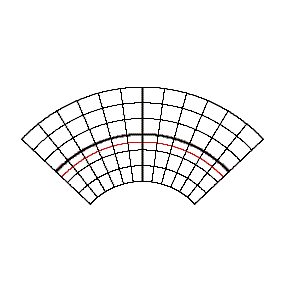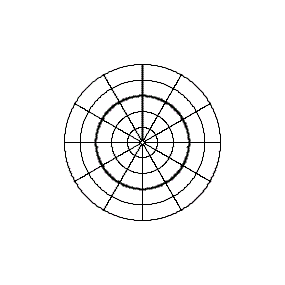
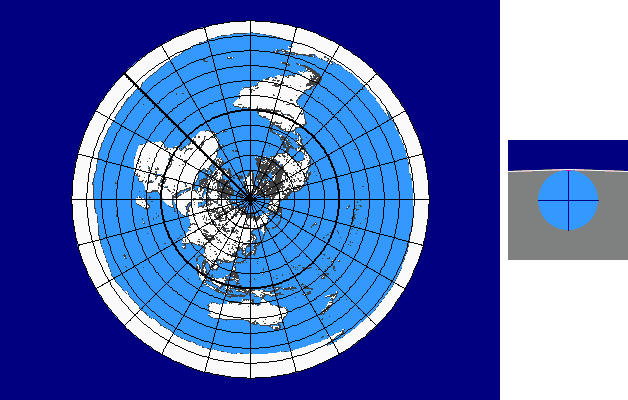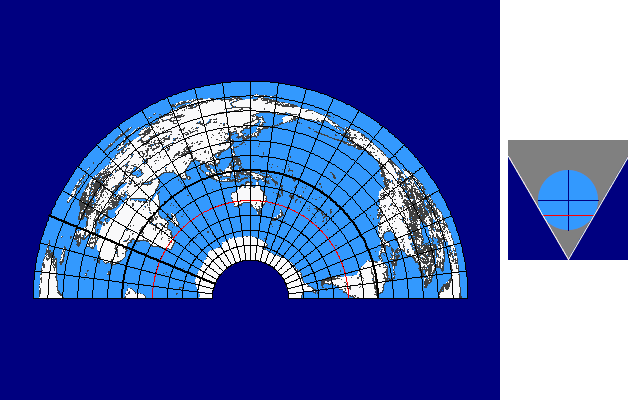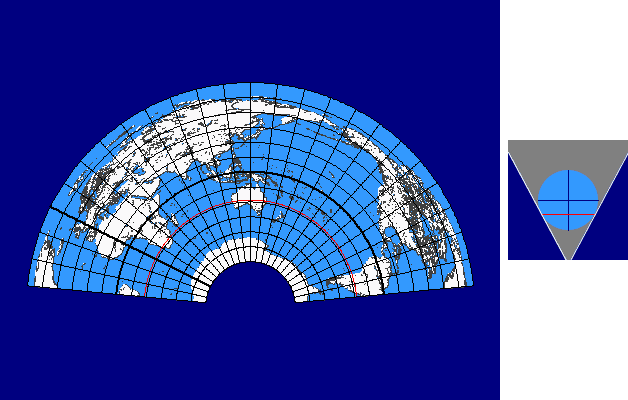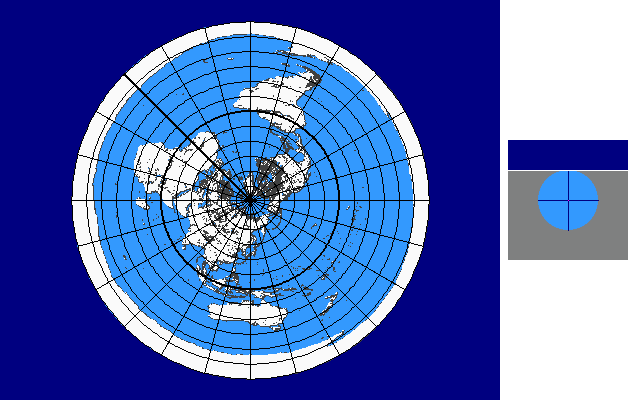
The perspective continuum is based on vertical-perspective azimuthal map projections. In this case the distance d between the point of perspective and the centre of the Earth is varied continuously as a multiple of the Earth radius.
For d = –1 the stereographic projektion is available, for d = 0 the gnomonic projection, for d = 1,4 the CLARKE „twilight” projection, for d = 1,5 the JAMES projection, for d = 1,71 the DE LA HIRE projection and for d → ∞ the orthographic projection.
Here you see the construction principle:
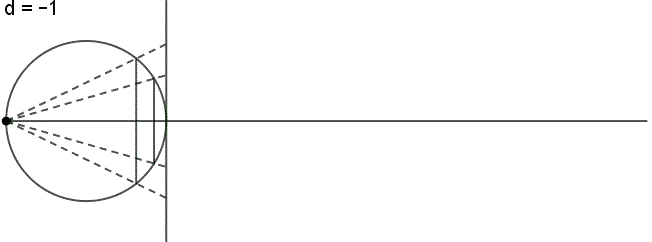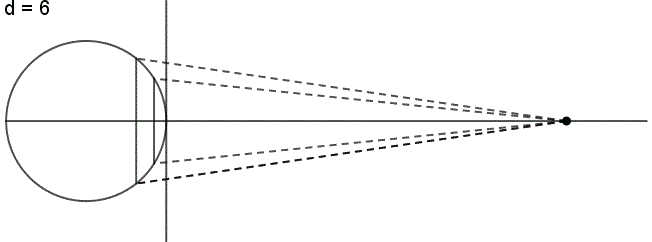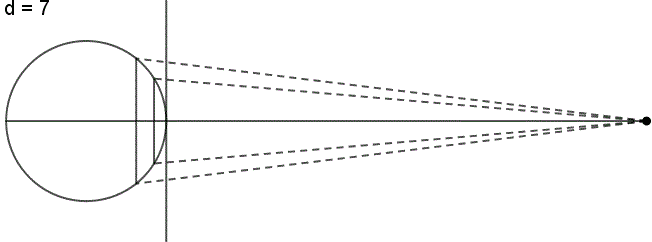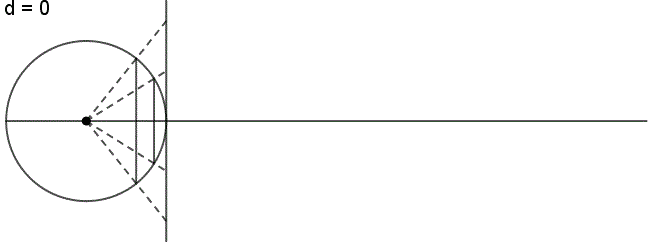
Conic Continuum
The conic continuum is based on the differentiation according to the type of the projection surface resp. auxiliary surface (plane, cone, cylinder). The basic idea of this continuum is a result of the imagination that plane and cylinder are „limit cases” of the cone (plane as infinite flat cone and cylinder as infinite high cone).
In case of the conic continuum the standard parallel v0 of a conic projection (with one single standard parallel) is varied continuously between 90° and -90°. The limit cases result as follows: for v0 = ± 90° we get the normal azimuthal projection and for v0 = 0° we get the cylindrcal projection.
The intersection-cylinder continuum is available for each of the three differential-geometrical variations:
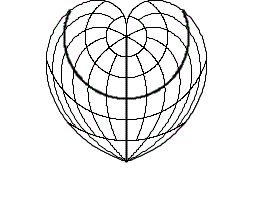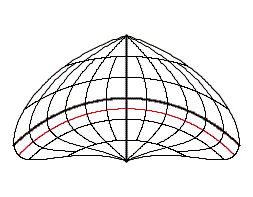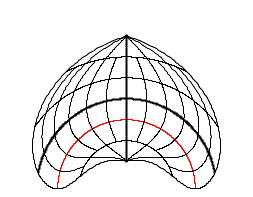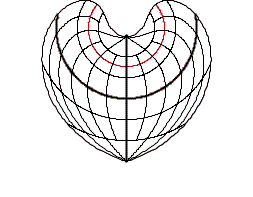
Pseudoconic Continuum
The pseudoconic continuum is based on the parallel-reduction preserving, equal-area projection of BONNE with the standard parallel v0 .
In case of the pseudoconic continuum the standard parallel v0 is varied continuously between 90° and -90° (as done for the conic continuum). As above-mentioned the limit cases also result as follows: for v0 = ± 90° we get the projection of STAB-WERNER and for v0 = 0° the projection of SANSON.
Here you see a preview:
Intersection-cylinder Continuum
The intersection-cylinder continuum is based on cylinder projections with two standard parallels ± v0 .
In case of the intersection-cylinder continuum the two standard parallels ± v0 , which are arranged symmetrically to the equator, are varied continuously between 0° und 90°.
The intersection-cylinder continuum is available for each of the three differential-geometrical variations:
.gif)